OBM2022 – Nível 2 – Problema 3

OBM2022 – Nível 2 – Problema 3

Problemas da OBM são conhecidos por sua dificuldade e beleza. Neste artigo, apresentaremos uma possível solução para o problema 3 do nível 2 da OBM 2022. Esse problema foi considerado o mais difícil do primeiro dia de prova.

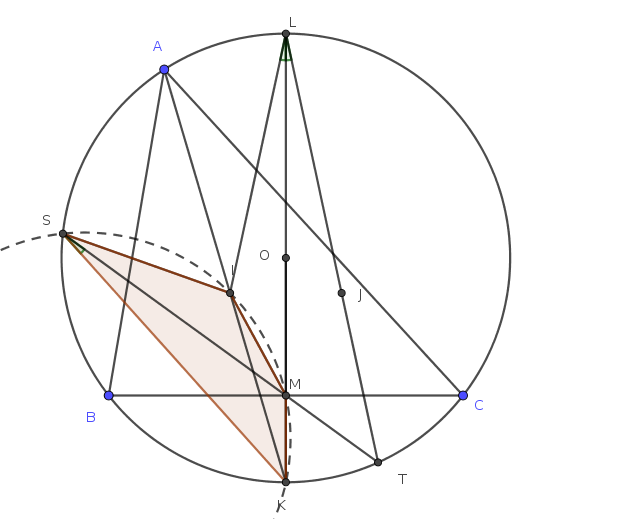
Solução. Em primeiro lugar, veja que \(\angle KSI = \angle KLT = \angle ILK\). (Essa última sendo verdade pela simetria entre \(I\) e \(J\) em relação ao diâmetro KL). Para provar que \(SIMK\) é cíclico, basta prova que \(\angle KIM = \angle ILK\) mas isso é equivalente a demonstrar que o círculo que passa pelos pontos I,M e K é tangente à reta IL. Usando potência de ponto, esse fato será verdade se e somente se \(KM\cdot KL= KI^2\). Porém, sabemos que \(IK=KC\). Logo, basta provar que \(KM\cdot KL= KC^2\). Porém, essa última igualdade é verdadeira pela relação métrica do triângulo retângulo \(KCL\) com altura \(CM\).